
Параграф 3. Задача 1
Заполните пропуски. 1) Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник — параллелограмм. 2) Если в четырёхугольнике

Параграф 3. Задача 10
Диагонали параллелограмма ABCD пересекаются в точке О. Точки М, N, К и Р — середины отрезков АО, ВО, СО и

Параграф 3. Задача 11
На сторонах параллелограмма ABCD отметили точки M, E, F и K так, чмо AM = AK = CE = CF.

Параграф 3. Задача 12
Точки M и K — середины сторон BC и AD параллелограмма ABCD. Докажите, что четырехугольник MNKP — параллелограмм. Дано: ABCD

Параграф 3. Задача 13
Дано: AM = CK, BO = OD, MO = OK. Доказать: ABCD — параллелограмм. Доказательство. Рассмотрим четырехугольник BMKD. MK и

Параграф 3. Задача 14
Дано: ABCD — параллелограмм, BE -биссектриса ∠ABC, DF- биссектриса ∠ADC Доказать: Прямая FE проходит через точку пересечения диагоналей параллелограмма ABCD.

Параграф 3. Задача 15
На сторонах параллелограмма ABCD отметили точки F, M, K и E так, что AF= CK, AE = CM. Докажите, что

Параграф 3. Задача 16.
На сторонах параллелограмма ABCD отметили точки N, M, K и R так, что ∠BAK = ∠DCM, BN = DR. Докажите,
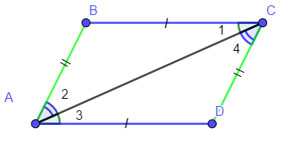
Признаки параллелограмма. Теорема 1. Доказательство
Докажите теорему: Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник — параллелограмм. Доказательство. На рисунке изображён четырёхугольник
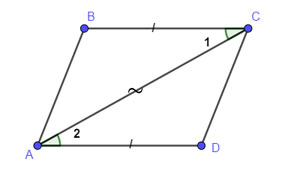
Признаки параллелограмма. Теорема 2. Доказательство
Докажите теорему: Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник — параллелограмм. Доказательство. На рисунке изображён
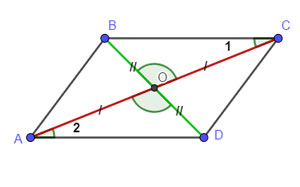
Признаки параллелограмма. Теорема 3. Доказательство
Докажите теорему: Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. Доказательство. На рисунке изображён четырёхугольник

Параграф 3. Задача 5
Отметьте знаком два из данных равенств, выполнения которых достаточно для доказательства, что четырёхугольник ABCD — параллелограмм. AB = CD АВ