Основные правила математики с примерами. 5 класс

Главная › 5 Класс › Основные правила математики с примерами. 5 класс

Содержание

Натуральные числа
Сравнение натуральных чисел
Свойства сложения
Формула пути
Корень уравнения
Правила решения уравнений
Отрезок, прямая, луч
Угол, биссектриса угла
Углы: развернутый, прямой, острый, тупой
Многоугольники. Равные фигуры
Треугольники: остроугольный, прямоугольный, тупоугольный
Треугольники: равнобедренный, равносторонний, разносторонний

Прямоугольник. Квадрат. Периметр
Умножение. Свойства умножения
Деление. Деление с остатком
Площадь. Площадь квадрата, прямоугольника
Объем. Объем прямоугольного параллелепипеда, куба
Дроби: правильная, неправильная, сравнение дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Преобразование неправильной дроби в смешанное число
Преобразование смешанного числа в неправильную дробь
Десятичные дроби: свойства, сравнение, округление
Десятичные дроби: сложение, вычитание
Десятичные дроби: умножение, деление
Среднее арифметическое
Процент

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число 0 меньше любого натурального числа.

0 < 1, 0 < 100

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

\underset{4}{\underset{⏟}{4352}} > \underset{3}{\underset{⏟}{999}}

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

3561 > 3559

Свойства сложения

Переместительный закон: $a + b = b + a$

15 + 10 = 10 + 15

Сочетательный закон: $(a + b)+c = a+(b +c)$

(23 + 15) + 25 = 23 + (15 + 25)

Формула пути

$S = V \cdot t$ $, г д е S — п р о й д е н н ы й п у т ь, V — с к о р о с т ь д в и ж е н и я, t — в р е м я, з а к о т о р о е п р о й д е н п у т ь S$

$S$ = 50км, $t$ = 2ч, $V$ = 25км/ч

$S = Vt$ , 50км = 25км/ч· 2ч

$V = \frac{S}{t}$ , 25км/ч = 50км : 2ч

$t = \frac{S}{V}$ , 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2 \cdot x + 10 = 16

x = 3 — к о р е н ь, т а к к а к

2 \cdot 3 + 10 = 16

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

\underset{с л а г а е м о е}{20} + \underset{с л а г а е м о е}{x} = \underset{с у м м а}{100} x = 100 — 20 x = 80

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

\underset{у м е н ь ш а е м о е}{x} — \underset{в ы ч и т а е м о е}{10} = \underset{р а з н о с т ь}{40} x = 40 + 10 x = 50

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

\underset{у м е н ь ш а е м о е}{50} — \underset{в ы ч и т а е м о е}{x} = \underset{р а з н о с т ь}{40} x = 50 — 40 x = 10

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

\underset{м н о ж и т е л ь}{x} \cdot \underset{м н о ж и т е л ь}{7} = \underset{п р о и з в е д е н и е}{56} x = 56 : 7 x = 8

Чтобы найти неизвестное делимое, надо делитель умножить на частное.

\underset{д е л и м о е}{x} : \underset{д е л и т е л ь}{8} = \underset{ч а с т н о е}{9} x = 9 \cdot 8 x = 72

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

\underset{д е л и м о е}{42} : \underset{д е л и т е л ь}{x} = \underset{ч а с т н о е}{7} x = 42 : 7 x = 6

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке $AC$ отметить точку $B$ , то длина отрезка $AC$ равна сумме длин отрезков $AB$ и $BC$ .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

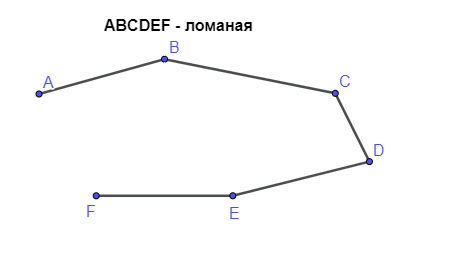
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

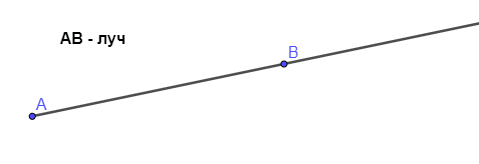
Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, $DC$ . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

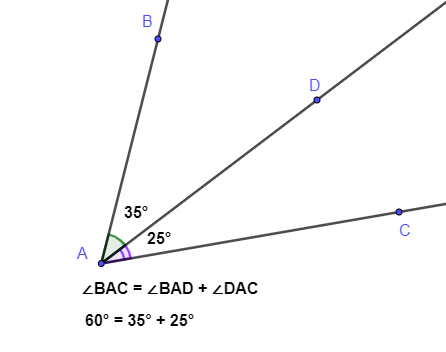
Свойство величины угла

Если между сторонами угла ∠ $ABC$ провести луч $BD$ , то градусная мера ∠ $ABC$ равна сумме градусных мер углов ∠ $ABD$ и ∠ $DBC$ , то есть ∠ $ABC$ = ∠ $ABD$ + ∠ $DBC$ .

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна $a$ , то его периметр $P$ вычисляют по формуле $P=3a$

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны $a$ и $b$ , то его периметр $P$ вычисляют по формуле $P=2(a+b)$

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна $a$ , то его периметр $P$ вычисляют по формуле $P=4a$ .

Умножение. Свойства умножения

Умножение

Произведением числа $a$ на натуральное число $b$ , которое не равно 1, называют сумму, состоящую из $b$ слагаемых, каждый из которых равен $a$ . В равенства $a \cdot b = c$ числа $a$ и $b$ называют множителями, а число $c$ и запись $a \cdot b$ — произведением.

$a \cdot b = \underbrace {a + a + \ldots + a}_b$
$5 \cdot 4 = \underbrace {5 + 5 + 5 + 5}_4$

Если один из двух множителей равен 1, то произведение равно второму множителю.

$1 \cdot 25 = 25\quad 25 \cdot 1 = 25$

Если один из множителей равен нулю, то произведение равно нулю.

$0 \cdot 25 = 0\quad 25 \cdot 0 = 0$

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

Переместительный закон умножения: $a \cdot b = b \cdot a$

$6 \cdot 3 = 3 \cdot 6$

Сочетательный закон умножения: $(a \cdot b )c= a( b \cdot c)$

$(17 \cdot 5) \cdot 2 = 17 \cdot (5 \cdot 2)$

Распределительное свойство умножения относительно сложения: $a(b + c)= ab + ac$

2 \cdot (3 + 10) = 2 \cdot 3 + 2 \cdot 10 3 \cdot 11 + 3 \cdot 4 = 3 \cdot (11 + 4)

Распределительное свойство умножения относительно вычитания: $a(b - c)= ab - ac$

2 \cdot (15 — 7) = 2 \cdot 15 — 2 \cdot 7 3 \cdot 10 — 3 \cdot 4 = 3 \cdot (10 — 4)

Деление. Деление с остатком

Деление

Для натуральных чисел $a, b, c$ равенство $a : b = c$ является правильным, если является правильным равенство

$b \cdot c = a$

15 : 5 = 3 -правильное равенство, так как равенство 5 · 3 = 15 верное

В равенстве $a : b = c$ число $a$ называют делимым, число $b$ — делителем, число $c$ и запись $a : b$ — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа $a$ правильными являются равенства:

$0 : a = 0$ ,

$a : a = 1$

Деление с остатком

$a=bq+r$ , где $a$ — делимое, $b$ — делитель, $q$ — неполное частное, $r$ — остаток, $r < b$ .

\underset{д е л и м о е}{154} = \underset{д е л и т е л ь}{50} \cdot \underset{н е п о л н о е ч а с т н о е}{3} + \underset{о с т а т о к}{4}, 4 < 50

Если остаток равен нулю, то говорят, что число $a$ делится нацело на число $b$ .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

$S=a^{2}$ ,

где $S$ — площадь квадрата, $a$ — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

$V=abc$ ,

где $V$ — объем параллелепипеда, $a$ , $b$ и $c$ — его измерения, выраженные в одних и тех же единицах;

$S = 2(ab + ac + bc)$ , где $S$ — площадь поверхности прямоугольного параллелепипеда.

$V=Sh$ ,

где $S$ — площадь основания параллелепипеда, $h$ — его высота.

Объем куба

$V=a^{3}$ ,

где — $V$ объем куба, $a$ — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

$\frac{5} {7},\quad \frac{8} {9}$

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

$\frac{{11}} {7},\quad \frac{{27}} {9},\quad \frac{7} {7},\quad \frac{{13}} {{13}}$

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

$\frac{3} {4} > \frac{2} {4},\quad \frac{5} {8} < \frac{7} {8}$

Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

$\frac{4} {5} > \frac{4} {7},\quad \frac{1} {8} < \frac{1} {5}$

Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

$\frac{4} {5} < 1,\quad \frac{3} {2} > 1$

Любая неправильная дробь больше любой правильной дроби.

$\frac{7} {5} > \frac{4} {5},\quad \frac{7} {7} > \frac{6} {7}$

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

$\frac{3} {7} + \frac{2} {7} = \frac{{3 + 2}} {7} = \frac{5} {7}$

Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

$\frac{4} {7} - \frac{1} {7} = \frac{{4 - 1}} {7} = \frac{3} {7}$

Сложение и вычитание смешанных чисел

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

$2\frac{3} {5} + 1\frac{1} {5} = (2 + 1) + (\frac{3} {5} + \frac{1} {5}) = 3 + \frac{4} {5} = 3\frac{4} {5}$

Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

$4\frac{6} {7} - 1\frac{1} {7} = (4 - 1) + (\frac{6} {7} - \frac{1} {7}) = 3 + \frac{5} {7} = 3\frac{5} {7}$

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

числитель разделить на знаменатель;
полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

\frac{22}{7} = с м е ш а н н о е ч и с л о ? 73 22 — 21 1 \frac{22}{7} = 3 \frac{1}{7}

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

целую часть числа умножить на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
эту сумму записать как числитель неправильной дроби;
в его знаменателе записать знаменатель дробной части смешанного числа.

5 \frac{2}{3} = н е п р а в и л ь н а я д р о б ь ? 5 \frac{2}{3} = \frac{5 * 3 + 2}{3} = \frac{15 + 2}{3} = \frac{17}{3}

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

2, 23 = 2, 230 = 2, 23000000 5, 50000 = 5, 50000 = 5, 5

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
после чего сравнить полученные дроби поразрядно.

С р а в н и т ь 5, 03 и 5, 0375 . 5, \underset{2}{\underset{⏟}{03}} = 5, \underset{4}{\underset{⏟}{0300}} и 5, \underset{4}{\underset{⏟}{0375}}; 5, 0300 < 5, 0375 .

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

все следующие за этим разрядом цифры отбросить.
если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

О к р у г л и т ь 5, 248 и 3, 952 : а) д о д е с я т ы х : 5, 248 \approx 5, 2; 3, 9 52 \approx 4, 0; б) д о с о т ы х : 5, 24 8 \approx 5, 25; 3, 952 \approx 3, 95 .

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми.

С л о ж и т ь 2, 5 и 3, 623 . 2, \underset{3}{\underset{⏟}{500}} и 3, \underset{3}{\underset{⏟}{263}}; 2, 500 + 3, 263 5, 763

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
выполнить вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми.

В ы ч е с т ь 3, 27 и 3, 009 . 3, \underset{3}{\underset{⏟}{270}} и 3, \underset{3}{\underset{⏟}{009}}; 3, 270 — 3, 009 0, 261

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

перемножить их как натуральные числа, не обращая внимания на запятые;
в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

У м н о ж и т ь 1, 5 и 2, 25 . 2 \times 2, 25 1 1, 5 + 1125 225 \cdot 3 3, 375 — количество цифр после запятой

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

У м н о ж и т ь 1, 235 н а 10, 100, 1000 . а) н а 10 : 1, 235 \times 1 \underset{1}{\underset{⏟}{0}} = 12, 35 б) н а 100 : 1, 235 \times 1 \underset{2}{\underset{⏟}{00}} = 123, 5 в) н а 1000 : 1, 235 \times 1 \underset{3}{\underset{⏟}{000}} = 1235, 0 = 1235

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

У м н о ж и т ь 512, 3 н а 0, 1, 0, 01 и 0, 001 . а) н а 0, 1 : 512, 3 \times 0, \underset{1}{\underset{⏟}{1}} = 51, 23 б) н а 0, 01 : 512, 3 \times 0, \underset{2}{\underset{⏟}{01}} = 5, 123 в) н а 0, 001 : 512, 3 \times 0, \underset{3}{\underset{⏟}{001}} = 0, 5123

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
выполнить деление на натуральное число.

Р а з д е л и т ь 24, 2 н а 0, 02 . 24, 2 : 0, \underset{2}{\underset{⏟}{02}} = 2420, 0 : 2 = 2420 : 2 = 1210 .

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Р а з д е л и т ь 25, 5 н а 10, 100, 1000 . а) н а 10 : 25, 5 : 1 \underset{1}{\underset{⏟}{0}} = 2, 55; б) н а 100 : 25, 5 : 1 \underset{2}{\underset{⏟}{00}} = 0, 255; в) н а 1000 : 25, 5 : 1 \underset{3}{\underset{⏟}{000}} = 0, 0255;

[ads2]

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

$\frac{\overset{с у м м а ч и с е л}{\overset{⏞}{15 + 25 + 20}}}{\underset{к о л и ч е с т в о ч и с е л}{\underset{⏟}{3}}} = \frac{60}{3} = 20$

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

Здесь

$V_{с р е д н я я} = \frac{S_{о б щ}}{t_{о б щ}} .$ 1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Ответ: 40 км/ч.

Процент

Процентом называют сотую часть величины или числа 1%= $\frac{1}{{100}}$

Н а й т и 4 % о т ч и с л а 20 . 20 : 100 = 0, 2 (0, 2 — э т о 1 % о т ч и с л а 20); 0, 2 \times 4 = 0, 8 (0, 8 — и с к о м о е ч и с л о) . И л и 4 % = \frac{4}{100} = 0, 04; 0, 04 \times 20 = 0, 8 .

Основные правила математики с примерами. 5 класс: 56 комментариев

Мария Матвеева:

28.08.2023 в 10:56

мне нравятся правила

Ответить
Зарина:

25.08.2023 в 11:58

Спасибо большое

Ответить
Аноним:

23.08.2023 в 00:22

Я не понимаю как я это запоминал до каникул

Ответить
Влад:

16.08.2023 в 21:07

Спасибо вам огромное! Лучше сайта не найти!

Ответить
1. Наталья:
  
  17.08.2023 в 12:41
  
  Пожалуйста )
  
  Ответить
чел:

30.05.2023 в 12:56

Супер !НО Я В ЖИЗНИ ЭТУ МАТЕШУ НЕ ПОЙМУ !!!!!!!!Сколько не учи все не пойму я на следующий день всё забуду

Ответить
1. Наталья:
  
  30.05.2023 в 15:14
  
  Бывает так, что ученик забывает, это особенности памяти) главное тренироваться
  
  Ответить
Алиса:

30.05.2023 в 10:55

Огромное спасибо вам большое спасибо вам лучше если бы не вы Я бы голову сломала

Ответить
1. Наталья:
  
  30.05.2023 в 15:11
  
  😊
  
  Ответить
Анна Валерьевна Крюкова:

28.05.2023 в 18:05

Спасибо!

Ответить
Кузнецова наталья Николаевна:

22.03.2023 в 11:00

Меня учили процент находить по другому х- 4,20-100, надо 20*4 /100 Получии80/100 ответ 0,8

Ответить
1. Наталья:
  
  22.03.2023 в 15:54
  
  Добрый день! Так как Вы написали , это решение через пропорцию. Это решение широко применяется на практике. Но пропорцию проходят в 6 классе, в 5ом считают процент выше указанным методом
  
  Ответить
Омар:

20.03.2023 в 18:39

Очень надеюсь что все я пойму дроби

Ответить
1. Наталья:
  
  21.03.2023 в 10:57
  
  Терпение и труд все перетрут! Обязательно поймешь, если постараешься
  
  Ответить
qwerty as:

15.03.2023 в 12:31

спасибо большое этому сайту мне он очень помог с математикой я сейчас в 5 классе……. и я совсем не понимала математику а спомощю этого сайта я теперь нормально понимаю в математике СПАСИБО БОЛЬШОЕ

Ответить
1. Наталья:
  
  15.03.2023 в 15:08
  
  Это здорово! Я очень рада, что сайт принес Вам пользу!
  
  Ответить
Тимур:

14.03.2023 в 09:58

Спасибо большое теперь буду с заполненой памятной😎🤓

Ответить
1. Наталья:
  
  14.03.2023 в 10:10
  
  Супер! Удачной учебы
  
  Ответить
Владислава:

13.03.2023 в 20:11

Спасибо, вы очень помогли!
Вчера наш класс сорвал урок, и неожиданно нам поставили контрольную но ВСЕМ ТЕМАМ ЗА ВСЕ ЧЕТВЕРТИ…
Ещё раз огромное спасибо Вам!

Ответить
Анжелика:

09.03.2023 в 08:52

Спасибо большое за помощь в мозгах.

Ответить
Влад:

05.10.2022 в 18:12

Завтра ВПР по математике но тема пятого класса а сейчас я в 6 классе но немного забыл материал 5-ого класса вот учу.Надеюсь на 4 или 5.Материал правильно написан все хорошо, спасибо

Ответить
1. Наталья:
  
  05.10.2022 в 19:57
  
  Удачи, Влад на ВПР. Спасибо за комментарий.
  
  Ответить
Виктория:

22.09.2022 в 12:53

спасибо большое. мне очень пригодится это на впр за пятый класс. я сама в шестом, но впр за пятый класс перенесли на осень, а за лето всë из головы вылетело. я очень благодарна.

Ответить
1. Наталья:
  
  22.09.2022 в 13:52
  
  Отлично! Удачи, Вика, на ВПР и в учебном году
  
  Ответить
Василиса:

19.09.2022 в 11:40

Спасибо , всё понятно

Ответить
Наталья:

11.08.2022 в 16:56

Пожалуйста, ребята! Удачи в новом учебном году!

Ответить
Полина:

11.08.2022 в 15:21

Спасибо большущее!!! Я закончила 4 класс, но из-за санкций у нас ВПР перенесли. Я всё забыла и вот всё опять вспомнила. Всё что важно пишу в блокнот. Советую) потому что перед контрольными можно всё повторить! Ещё раз спасибки ☺️

Ответить
К.П.:

08.07.2022 в 16:05

Спасибо, все очень понятно!

Ответить
Кира:

05.07.2022 в 13:40

Спасибо большое!
Я всё хорошо запомнила и написала все к.р.

Ответить
даниил:

08.06.2022 в 14:19

спасибо огромное мне понятней чем в учебнике по математике я в 5 классе…..мне просто тесты здавать надо

Ответить
1. Наталья:
  
  19.06.2022 в 10:01
  
  Даниил, надо работать и делать все заранее. Удачи
  
  Ответить
Елена:

29.05.2022 в 03:12

Всё очень круто. Спасибо.

Ответить
Таисия:

10.05.2022 в 06:42

Большое спасибо вам ! Я по учебнику вообще правила не понимала. А завтра мне писать теоретический зачёт по правилам.

Ответить
Лариса:

22.03.2022 в 18:16

Все очень понятно и кратко. Ребенок готовится к устному зачёту.

Ответить
ксения:

27.10.2021 в 13:19

очень понятно и самое главное кратко я все поняла спасибо. за время лок дауна нужно как раз подтянуть оценки по 5 классу так как я в шестом.

Ответить
Flimbu_lili:

02.09.2021 в 22:04

Прекрасно, повторила материал очень быстро и понятно, спасибо!)

Ответить
Авдей:

16.08.2021 в 12:06

Спасибо, Помогли)

Ответить
надя:

29.07.2021 в 14:19

спасибо огромное за ваш труд

Ответить
Наталья:

17.07.2021 в 10:23

Пожалуйста! 😊

Ответить
Зинаида:

17.07.2021 в 08:49

Огромное спасибо вам Наталья Владимировна! Благодаря вашей подборки правил мы с внучкой в летний период повторили кратко основы математики .Исправили ошибки, закрепили правильность работы с формулами площадей ,периметров,
объемов.

Ответить
Аркадий:

12.07.2021 в 12:58

Спасибо, Вы очень помогли мне ! Все правила написаны кратко и по существу! Огромное СПАСИБО!!!

Ответить
Джалала:

30.06.2021 в 14:26

Спасибо большое.Повторяли 5 класс,все чётко, кратко и понятно.👏

Ответить
Али:

26.05.2021 в 20:24

Спасибо большое! Пропускал математику в школе, решил найти краткое изложение 5 класса, так как в школьных книгах много воды. И вот так повезло, наткнулся на ваш сайт, и за сегодня прошёл весь 5 класс. Всё понятно и без вопросов.

Ответить
Олеся:

20.05.2021 в 13:39

спасибо!! как раз у меня завтра годовая к/р!

Ответить
Наталья:

09.05.2021 в 15:20

Ребята, спасибо за классные комментарии )).
Я рада, что материал оказался полезным.

Ответить
ярослава:

09.05.2021 в 14:38

очень понятно объяснили проценты,дав только одну формулу из 3 ,спасибо.я в жизни эту дебильную матешу не пойму

Ответить
Юлия:

05.05.2021 в 07:38

Спасибо!!!! Очень помогли!!!! Материал изложен чётко, кратко и понятно. Супер!!!!

Ответить
Елисей:

24.04.2021 в 10:24

Спасибо у меня скоро контроша надеюсь здам хорошо

Ответить
Руфина:

15.04.2021 в 13:53

Спасибо большое за ваш труд вы всё понятно и правильно обяснили

Ответить
Елена:

19.03.2021 в 03:46

отличный материал! спасибо!

Ответить
Арт:

09.10.2020 в 16:43

Очень классно.

Ответить
вероника:

08.10.2020 в 16:26

Супер!

Ответить
Амина:

17.09.2020 в 00:26

Спасибо огромное ! У меня завтра впр , и я надеюсь я получу 5 😇💖

Ответить
Наталья:

16.09.2020 в 18:41

Пожалуйста! Я очень рада, что Вы высоко оценили мой труд.

Ответить
Эл:

16.09.2020 в 14:38

Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!

Ответить
Камил:

21.08.2020 в 21:14

Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли

Ответить